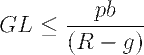少々偏見混じりのレベルの低い雑感です。あらかじめ断っておくことにします。
さてさて、最近でこそ文系とおもわれることも多くなったyuukomaです。「物理系だったんですね」とかいわれることもいまや珍しくもありません。
それでも一応というか結構な割合でバリバリ理系色強い部類に属しているかと思います。
そんな文系的なイメージは職業柄まといついているものなのでしょうが、それにしてもいわゆるこの手の文系業種でだいたい学んでるであろう「経済学」、この教科書がほんと昔からキライでそれはいまでも変わりありません。
数式が多く意外なんて言われる経済学の教科書、もっともバリバリ理系な人から見るとびっくりするくらい簡単な式ばかりですが、それらがどうもいわゆる「暗記」を求められるような書き方をされていて、ほんと「文系」だねって思うわけです。
理系、数学とか物理=公式の暗記ってイメージが強いんですかね。
あんまりいい例ではないのですが…。
今日ネット見つけた次の記事、
記事の内容よりもこの式がすごい気になったんです。
政府債務(対GDP)≦ pb ÷(R-g)
項のそれぞれの意味についても引用させていただきます。
右辺のpbは「基礎的財政収支(対GDP)の上限値」、Rは「国債金利」、gは「経済成長率」を表す。また、この「pb」(=基礎的財政収支の上限値)は観測不可能な変数で、政府が増税や歳出削減で達成可能な基礎的財政収支(対GDP)の限界(いわゆる「財政限界」)を意味する
この式が一見するとなにを意味しているのかさっぱりわからない。
ゆっくり考えれば、慣れていればすぐわかるのかもしれませんが、凡人の僕にはすぐには意味がわかりませんでした。
こういうとき、理系の人はだいたいイメージを掴むために、式変形するんですよね。
実際やってみます。とりあえず両辺にGDPを掛けてからスタートしたとします。
(※ 政府債務をGLとしました。いちおうR-g>0としました)
ここまで持ってくると、
政府債務・実質金利っぽい金利 ≦ 基礎的財政収支
つまり、
基礎的財政収支が、将来の債務の(厳密には実質金利じゃないけどそれっぽい)実質的な利払い額以上
って意味になりますよね。これだったらわかりやすいんじゃないかと。ほんのちょっとした違いなんですが、こうじゃないと理解できない「センス」なんです。
僕はこうして初めて、この記事でいうところの、
「市場が要求する政府債務の再構築の幅」(対GDP比)
を理解できました。
もっとも経済や金融の人が大好きな「現在価値」という概念に慣れていればすぐに理解できるのかもしれません。
しかし、この微妙なセンスの差を通した理解っていうんですかね、いずれにしても「経済学っぽい理解の仕方のセンス」が残念ながら自分にはないし、勝手な想像ではありますが、理系出身者の多くにはないんじゃないかと思っています。
とはいえ、確かに本文の中で「若干粗い試算」と断ってあるし、文字数や紙面の限られたウェブの記事なのできちんとした経済学の教科書にはおそらく書いてあろう説明を省略したのだと思いますが、自分の経験からすると、多くの教科書はトップダウン的に「これはこの数式で表せる」的なものが多い気がします。
そんなことはないって反論もあるでしょう.
でも、実際自分の経験では、経済学部のひとに数式の意味をきいてもいわゆる「暗記的」な形での回答しかかえってこないことばかり。
あるいは証券アナリスト試験といったたぐいの経済系の資格においても、その試験対策用テキストなどでは数式はほとんどこの手の「暗記型」扱いです。
僕は大学で経済学の授業とか出たことないけど、授業でも「暗記ありき」で数式を教えているんでしょうかね…。
これでは確かに数学ができない人が多いのも頷けます。
きちんと意味を考えながら式変形をして理解することができないから、本質が理解できず、結果数式嫌いを生んでいるのかもしれません。
いわゆる金融のプロ(笑)ですらそういう人が多いことはそれほど珍しくはないと思います。
しかし、数こそ少ないですが、世の中には以下の本のように「アンチ暗記型数式」的なものもあります。
縄田 和満
東洋経済新報社 2003-03
売り上げランキング : 323023
理系脳の自分にとってこのような本があることは、数少ない救いになっています。
最後に。
こうした話を書くときっと「単なる経済学の勉強不足、理解不足」という反論がきそうです。
がしかし、自分の言ってる式とか理解できないと「勉強不足」だとかいうひとって、数学や物理出身者ではほとんど見かけません。
それがあまりにも基礎的すぎることなら別ですが、基本的にはなぜそういう式が導出されるのか、どういう意味を持つのかを解説してくれます。
こういったところも「暗記型」な感じがします。