フランスの最も美しい村巡り(巡回セールスマン問題)を量子コンピュータっぽく最適化しようとしましたが、結局うまくいかなかったです。でもとても勉強になりました。
量子コンピュータは既に存在する
量子コンピュータは、最近では一般のニュースでも取り上げられるくらい市民権を得つつある気がします。その言葉自体を聞いたことがある人は多いのではないでしょうか。MITテクノロジーレビューでも、2017年注目の技術の一つとして掲げています。

出所:10 Breakthrough Technologies 2017: Practical Quantum Computers – MIT Technology Review
そんな量子コンピューターですが、僕が生きている時代には実現なんてしないとか思っていたのです。しかし、2015年12月8日 のGoogleとNASAによる研究発表がおそらく近年では一番の衝撃だったことでしょう。このニュースを聞いて、実際に量子コンピューターがここまで開発されていたのかと驚いたことを覚えています。
【主なメディアでの関連ニュース(英語メディアのみ)】
もちろん量子コンピューターが実在している自体も驚きでしたが、それだけでなく、ごく限られた条件とは言え、現時点でも従来型のコンピューターよりも1億倍も速いということにも驚きました。ただ正直な処、1億倍といってもピンとこないですよね。ざっくりしたたとえですが、[highlight]「これまで1億秒=3年2ヶ月くらいかかっていた計算をたったの1秒でできてしまう」[/highlight]ということです。こう考えると確かにものすごいことです!もっともそんな3年もかかる計算って一体何?とは思いますけどね笑。
量子コンピータを実現に導いたアニーリングとは
さて、このときにGoogleとNASAが使っていたのが、D-Waveシステムと呼ばれる量子コンピュータです。この量子コンピュータは、これまで長年研究されてきた「量子ゲート方式」ではなく、「量子アニーリング方式」というもので構築されているのが最大の特徴です。
量子アニーリングとは、組み合わせ最適化問題などを解く時やサンプリングを行う時に、量子統計力学を使う、というものです。基本的なしくみは、学部レベルの物理の知識、特に統計力学と量子力学の知識があれば、この仕組みを十分理解できるはずです。
もっと詳しく知りたい方は、この量子アニーリング研究の第一人者、東工大教授の西森さんのページが最も参考となるでしょう。彼のサイトはこの世界を知る上では必見だと思います。
参考サイト:量子アニーリング(西森秀稔)
より一般向けのレビューとしては、同じく西森さんが執筆した以下の本も大変参考になります。
Amazon.co.,jpへのリンク: 量子コンピュータが人工知能を加速する
特に近年の動向を知る上で大変参考になりました。
量子コンピューターをつくってしまった会社
そして、量子アニーリングのロジックを実現するコンピュータを実際に作ってしまったが、こちらのカナダのとあるベンチャー企業[highlight]「D-Wave Systems Inc.」[/highlight]。やはりというか物理学者が起業したとのことです。

GoogleとNASAの例の論文では、このコンピューターを使っての計算を、「物理的量子アニーリング」(Physical Quantum Anealing)と読んでいます。どうして「物理的」というのかはこのあと説明予定の量子モンテカルロ法との対比でよりイメージが湧くかと思います。
今のところ、量子アニーリングで取り扱える、計算できるものは、組み合わせ最適化、クラスター分解といったごく一部のアルゴリズムだけのようですが、今後は人工知能、機械学習、とりわけ最近流行り力技の代名詞?ディープラーニングで力を発揮する可能性があると期待されます。なにせ1億倍のスピードですからね。既にある物理理論とのアナロジーでいろんな応用が生み出されていくことを期待したいです。
量子コンピュータの応用技術、ソフトウェアの開発も進んでいる
量子コンピュータD-Waveの登場により、その活用方法について考え始めた会社もすでに存在、[highlight]「1QBit」[/highlight]という会社です。こちらもカナダの会社だとか。

写真の出所および詳細はこちら:Home – 1QBit
この会社のウェブサイトでは、すでにいくつかホワイトペーパーを後悔しています。直近のリリースではファイナンス関係が続いていることは注目です。例えば「Quantum-Inspired Hierarchical Risk Parity」ではアセットアロケーションの話題を、そして「Finding Optimal Arbitrage Opportunities Using a Quantum Annealer」では為替の裁定取引の話題を取り上げています。ファイナンスは、量子コンピューターの応用分野の有力候補のひとつのようですね。ビジネスにもつながりやすいですからね。
実際、GoogleとNASAの例の論文もポートフォリオ最適化問題をもとに、コンピューターや計算方法のスピード差を計測したとしています。
(ちなみにこの論文をくまなく読んでいくとこの論文では用いなかったが、彼らはこのポートフォリオ最適化問題をもっと高速に解けるアルゴリズムを発見したらしいです。「 量子コンピュータが人工知能を加速する」より)。
ファイナンスであれば、一応その業界で仕事している関係上、大変興味を持っているのでもう少し深掘りしたいところではありますが、最近はあまり仕事に近いことを書くと面倒になることもあるのでやめておきます。
自宅でも量子コンピュータっぽいことができる
そんなワクワクなD-Waveシステム、さすがに現時点では個人でこれを使うことはできませんが、一方で量子アニーリングの概念は、何もこのコンピュータでなくても、従来型コンピュータ、つまりいま手元にあるPCでも実現することはできます。それは、[highlight]量子モンテカルロ法(経路積分量子モンテカルロ法, Quantum Monte Carlo Simulation)を利用する方法[/highlight]です。
なお、組み合わせ最適化の問題を解く手法としては、従来より、シミュレーティッドアニーリングという、どちらかというと古典的な手法、それでも物理理論のアナロジーにもとづいて最適化問題を解く方法が知られていました。
例の前述のGoogle&NASA論文によれば、ビット数があまり大きくなければ、古典的なアニーリング、すなわちシミュレーティッドアニーリング(SA)の方が、量子モンテカルロ法(QMC)による量子アニーリングよりも早く計算できゆようですが、ビットサイズが1,000近くになると量子モンテカルロ法の方が速くなるようです。
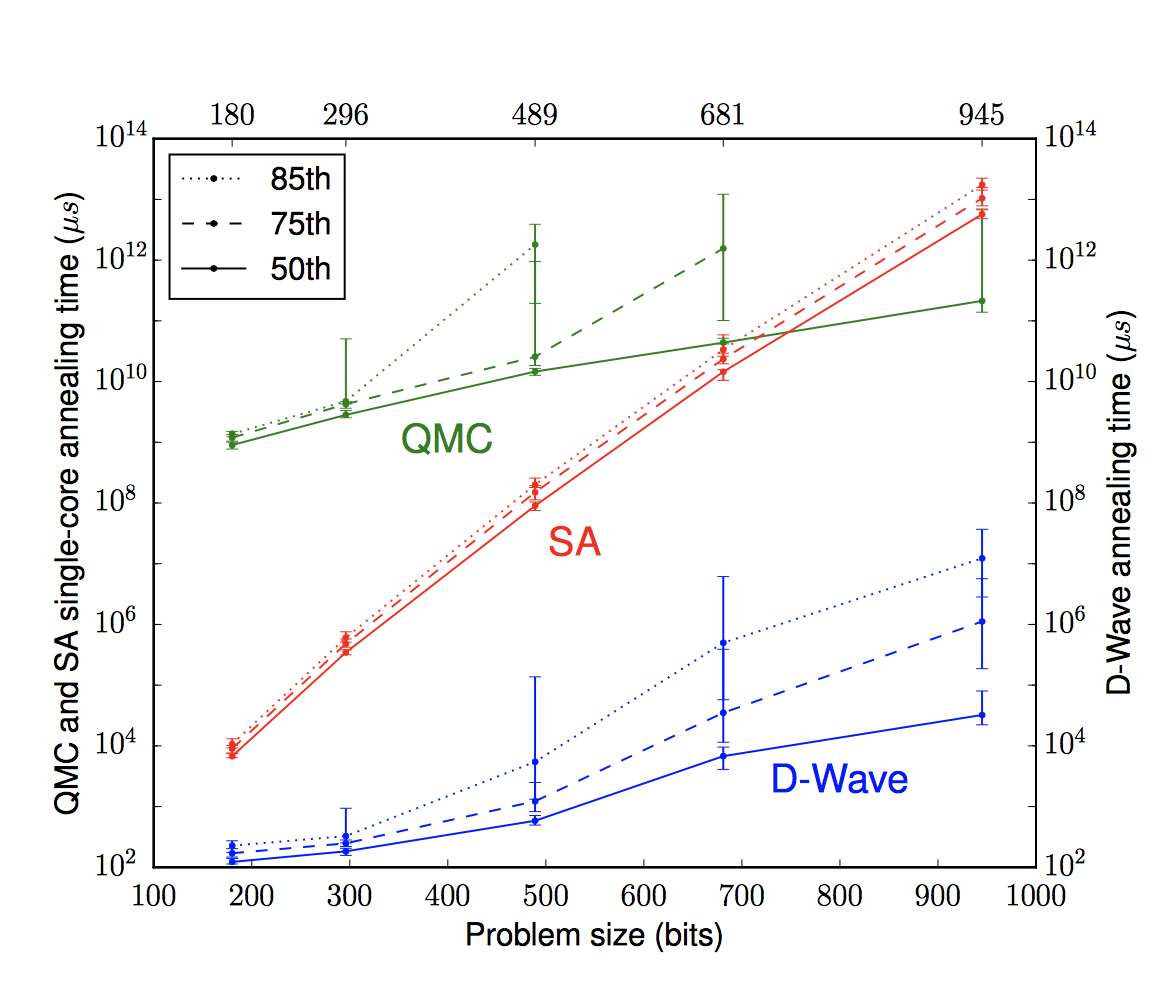
出所:What is the Computational Value of Finite Range Tunneling?より
つまり、量子モンテカルロ法を用いれば、たとえ従来型のコンピュータであっても、ビット数が多くなるにつれて、そのスピードが活かされる、ということです。この辺りは、スモールデータだとイマイチだがビッグデータだとパワフル、というhadoopにも似た性質ですね。
ちなみに例の1億倍速いという数字は、シミュレーティッドアニーリングとD-Wavesによる物理的量子アニーリングの比較からきていると思います。また、量子モンテカルロとD-Wavesの結果がビット数を増やしてもその計算スピードの差は、シミュレーティッドアニーリングの計算時間が急激に上がっていくのとは対照的に、ビット数にあまり依存しないということも興味深いですね。
もちろんD-waveを使うに越したことはありませんが、それが使えなくても量子アニーリングの研究は可能だということです。少なくとも組み合わせ最適化、クラスター分析以外にも汎用化できる可能性を探るにはもってこいでしょう。誰でも手軽にできますからね。
自宅で量子コンピュータ風に旅行計画最適化にチャレンジ
せっかくなので、この量子アニーリングへの理解を深めるため、量子モンテカルロ法を用いてちょっと遊んでみることにしました。具体的な素材としては、以前行ったことがある、イタリアの最も美しい村巡りの最適ルート作成問題を選んでみました。
以前計算した時のサンプルは、「イタリアの最も美しい村巡り、南イタリア&シチリア編」でした。
さらにせっかくなので、今回の検証では、イタリアの最も美しい村ではなく、このサイトの本命でもあるフランス本土にある「フランスの最も美しい村」で量子モンテカルロを実行してみることにしました。そして、実際に量子モンテカルロ法がどの程度まで精度なのか、そして解くまでの時間はどの程度なのかを、以前造ったプログラムでの結果と比較することで判断してみます。
計算はPythonで行えます
この従来型コンピュータを利用した量子モンテカルロ法は、RやPythonといったプログラムで簡単に実装できます。こちらに具体的なPython のコードがありました。量子アニーリングの簡単な解説もあるので、予備知識がないと厳しいとは思いますが、よい復習にもなりました。
参考にしたサイト:量子アニーリングで組合せ最適化
基本的にはここに書かれているコードをそのまま利用しますが、ごく一部個人的にはcostと書かれているところがちょっと気に入らなかったのと、(ロジック解説部分の)分配関数とpython内の関数との対応がぱっと見わかりづらかったので、まず分配関数を次のように書き換えてその意味を解釈し、コードの部分costを、この分配関数のexpの肩 (-βでくくった中身)と一致することがわかるように、次のように書き換えました。
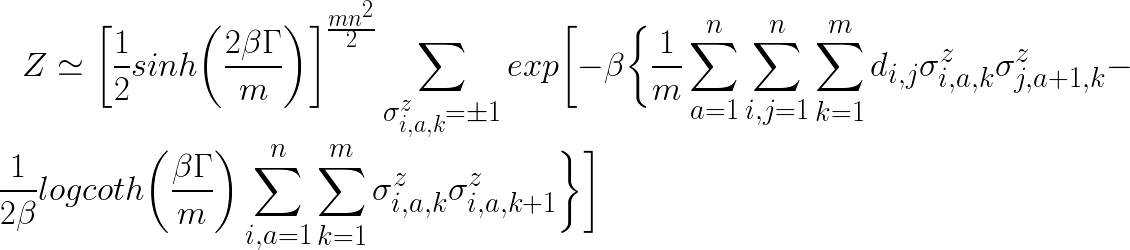
要するに量子効果を加味した場合の有効エネルギーが以下のように表されるので、
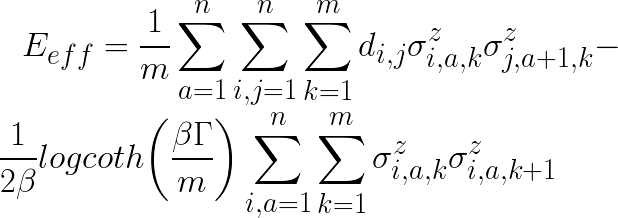
これがわかりやすいようにコードにも反映させただけです。計算しようとしていることは同じです。
Google direction APIで取得した位置情報を利用
前回同様、村間の距離や移動時間については、GoogleマップAPIを利用して距離・移動時間マトリックスを作り、これを利用しました。都度APIを利用してデータを取ることもできるのですが、確か短時間にAPIを利用しすぎると制限を超えてしまいエラーがでてしまう恐れがあったので、あらかじめ必要な分だけAPIを実行し、先に各村間の距離・移動時間マトリックスを造ることにしました。
なお、現実的には移動距離よりも移動時間を最適化したほうがよいと思っているので、移動時間を最小にする解を求めることにします。これもAPIから取得可能です。Google Mapの移動時間って本当に正確ですからね。
今回あらかじめ取得した2点間の距離、移動時間、移動ルートなどが記録されたjsonは、対象が158箇所(出発点としてパリのシャルル・ド・ゴール空港を追加)あるため、取得しなければいけない位置情報のjsonファイルは、158×157 / 2 = 12,403個。
しかし、Google Maps Direction API は一日に2,500リクエストまでが無料、それ以上使う場合は、1,000リクエストにつき0.5ドルかかります。5日かけて取得しても良かったのですが、面倒なので一気に12,000以上リクエストをしてしまいました。500円程度の課金、まあ趣味だしよしとしましょう。
さらに今回は、以前のように単に都市間を直線で結んで表示するのではなく、Google Maps上に実際の移動ルートも反映してみました。つまり、最適ルート内に各村間を結ぶ線を、Google Maps Direction API から取得したjsonの routes.legs.steps[i].polyline.points の値をデコードした後、Google Maps javascript API でpolylineオプションを実行してみました。
詳しい使い方はhttps://developers.google.com/maps/等を参照にしてみてください。
Googleのサイト:Interactive Polyline Encoder Utility
それ以外にもウェブにいろいろ情報が転がっております。「Google Maps API エンコードデータ デコード」などでググるとよいでしょう。ちなみに僕は以下のサイトを参照にさせていただきました。
参考にさせていただいたサイト:Google Static Maps APIの使い方まとめ!画像地図を作ろう!
ということで、まずは以前のプログラムで計算した最適化ルート結果がこちらです。
最適化ルート従来版:フランスの美しい村巡り 最適ルート2017年
トータル移動時間は、614,345秒=7日2時間39分5秒となっています。
ただ、このプログラムだとスタート地点=ゴール地点となっていません。コードを改良しないと出来ないみたいですが、僕のコード書きの実力では少し時間がかかりそうなので今回は諦めました。
量子モンテカルロの結果、計算時間がかかりすぎでした
さてその結果は、と行きたいところでしたが、あまりにも時間がかかりすぎて途中で計算を挫折しかかりましたがなんとか求めてみました。従来のプログラミングでは数秒だったのに対し、こちらの量子モンテカルロによる計算には、いろいろなパラメーター条件を課して、10時間、20時間かかるのはザラでした。計算したPCはiMac 27inch、スペックは以下の通り。
これだけ時間がかかっては、以前イタリアの村最適化で用いた方法(※おそらくシミュレーテッドアニーリングと思われる)とは比べ物になりません。この程度では全く使い物になりません。僕が3年前にイタリアの美しい村巡りで使用したpythonのライブラリがすごすぎるとも言えるでしょう。
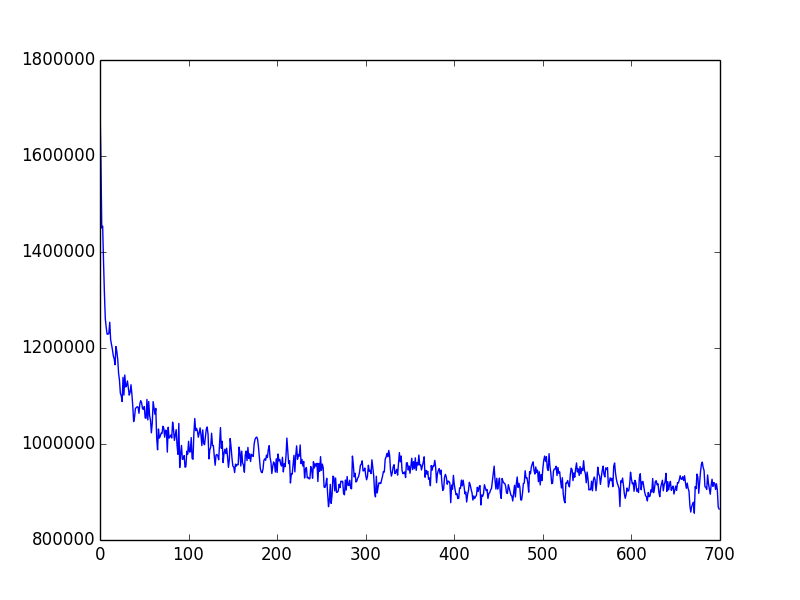
とにかくパラメータを変えたとしても、何度やってもすべての村をまわるのにかかる時間が85万から90万秒を下回ることがありません。だいたい10万秒くらいまでは順調に落ちる=移動時間が小さくなるのですが、そこからは何度モンテカルロしても先に進みません。以前のものが61万秒ですから、工程の長さは1.5倍程度。全然だめですね。
ちなみに以下のグラフは手元で計算した量子モンテカルロの結果。横軸は断熱的に磁場をゼロにする回数(アニーリング反復回数?)、縦軸は総移動時間(秒)です。以下の例では、もうどんなパラメーター条件だったか忘れてしまいましたが、だいたいどれも似たような振る舞いだったので、イメージ図として載せておきます。
以下に従来版vs量子版の結果を載せておきます。左側が3年前に使ったプログラムで、右側が今回量子モンテカルロ法で計算したもの。その差は見た目だけでも歴然であることがわかります。量子版は、特に美しい村が集中するフランス南西部のルートがぐちゃぐちゃです。
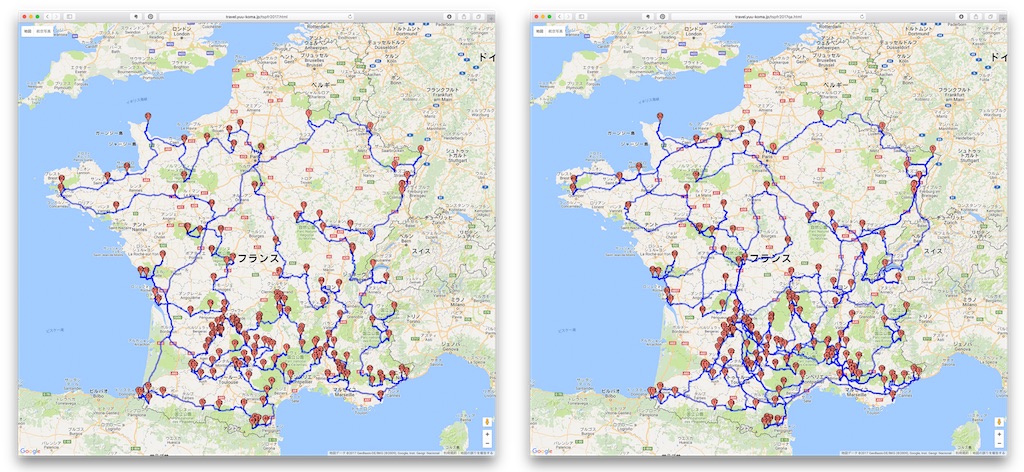
一応、量子版の最適化ルートの結果を反映させたサイトを公開しておきます。jsonが重いせいなのか開けるときと開けないといがあるみたいです。
最適化ルート量子版:フランスの美しい村巡り 最適ルート2017年
しかし、もう少し理論を理解して適切なパラメータを定める必要があるかもしれません。。
量子アニーリングのメリットは、ここで利用する基底状態が、各種の撹乱に対して比較的安定な点であるということです。例えば、基底状態と第一励起状態の間のエネルギーギャップに対して温度が十分低ければ、温度効果(熱撹乱)は無視できますが、逆にこのエネルギーギャップが小さいと、温度効果は無視できない、すなわち基底状態から励起状態への遷移が無視できなくなるため、温度を十分高く選んでゆっくりと系を制御しないと望み通りの基底状態を得ることが難しくなるそうです。
したがってより厳密に計算するのであれば温度と系のエネルギーギャップのバランスを図りつつパラメータの水準を決めるべきですが、今回はこれは十分に考慮できていません。このあたりのチューニングにはもっと精査する余地があったでしょう。しかし、残念ながらここまで探る余裕も能力もありませんでした
しかし、今回は失敗してしまったものの、あらためてこの量子モンテカルロの優れているところをあげるとすると、それは、ビット数が増えても、結局のところ、計算回数は、高々1回あたりのモンテカルロ・シミュレーション回数×アニーリング試行回数ですから、計算を終えるまでの時間がこれによってビット数が増えても指数関数的には増えないことだといえます。この点が従来の計算方法と比べると大きく違う点であり、このことはGoogleとNASA論文でも指摘されています。
量子モンテカルロのライブラリーがあったらいいな→ありました!
その一方で、Pythonのコードを工夫する余地はあるかもと思いました。そう思って、例えばGoogleが公開している機械学習ライブラリーTensor Flow量子モンテカルロのライブラリーとかあったらいいなと、そもそもこの量子コンピュータはGoogleも積極的に研究しているわけですから。しかし現時点ではどうやらなさそうでした。
しかし、その代わりに例の1Qbit社がこんなSDKを密かに公開していることを発見。
1Qbit SOFTWARE DEVELOPMENT KIT: 1Qbit SOFTWARE DEVELOPMENT KIT
前述のホワイトペーパーをよく読んでみると、ここでの研究でもこのSDKを用いたと書いてありました。
このSDKを利用するにはアカウント登録が必要ですが、無料でできます。
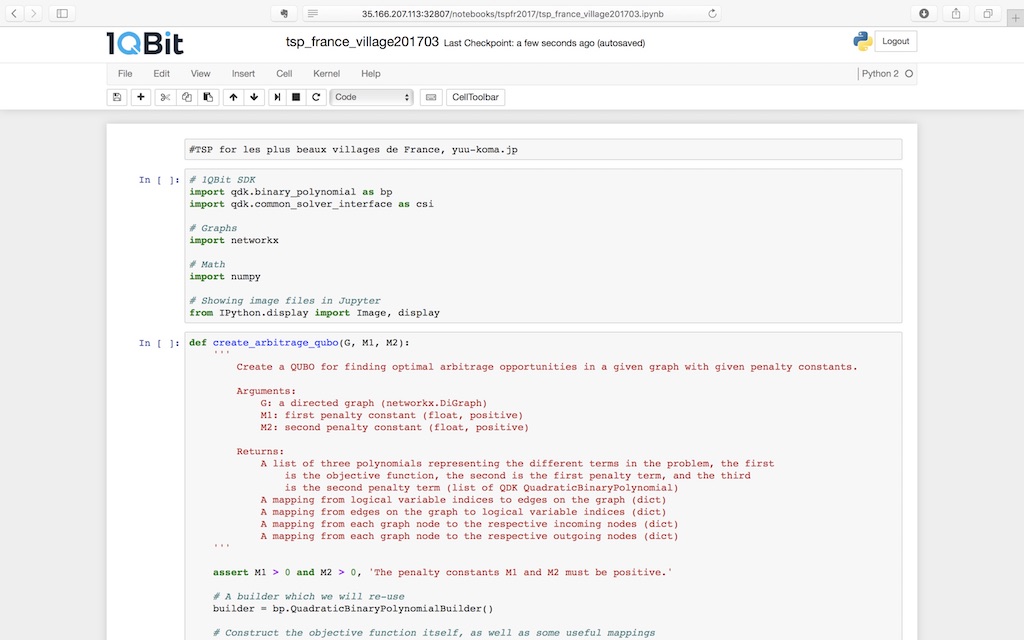
ということでサインインして早速使ってみようとしたのですが、ローカルの端末にはインストールできませんでした。なぜインストール出来ないのかは、どうやらGithub上にはもうこのSDKのリポジトリが存在しないからみたいです。しかし、[highlight]「 1QBit’s interactive Jupyter Notebook」[/highlight]を利用すればブラウザ上でこのSDKを利用できるようなので、こちらで試してみることにしました。

いくつかのサンプルコードが入っています。分析に必要なpythonライブラリはすでにインストールされているので便利。そして、思った以上にサクサク動いて使いやすいです。試しにこれらのサンプルコード動かしてみるとすぐに使い勝手が実感できます。
なお、一回ログオフしてしまうと新規で作成したファイルが消えてしまうので、ログオフする前にサーバーからダウンロードしておく必要があります。ダウンロードファイルは、拡張子が.htmlや.jsonだったりしますが、ダウンロード後にこれらの拡張子を削って.pyとか.ipynbとしておけばOKです。再度ログインした時、この.pyとか.ipynbのファイルをアップロードすれば問題ありません。
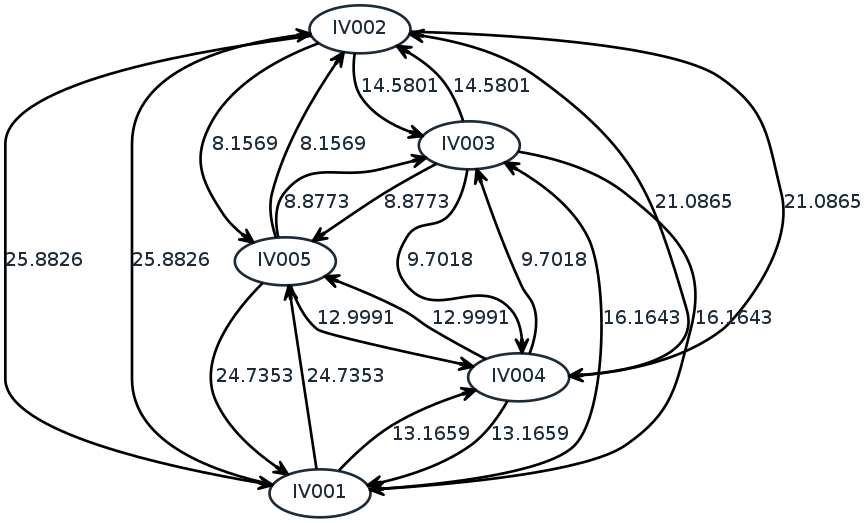
さて巡回セールスマン問題を考える上で、1Qbitがサンプルとして公開しているpythonの中で、今回最も参考になりそうだったのが、前述した[highlight]「Finding Optimal Arbitrage Opportunities Using a Quantum Annealer」[/highlight]というホワイトペーパーで実際に用いられたコード。このペーパーの対象は為替のアービトラージの最適化ですが、各為替間のレート=コンバージョンレートがちょうど村の間の地図に相当するので、入力データをコンバージョンレートから距離情報に置き換えれば、巡回セールスマン問題に適用できるかもしれないと考えました。とりあえず適当に5地点のデータ(IV001からIV005、数字は適当)を入れて、サンプルプログラムどおりにチャート図を作ったのがこちら。
ただし、このペーパーで使用している目的関数の中では、すべての村は1回のみ訪れるという制約条件=ペナルティー項は考慮されていますが、[highlight]「1つの閉じたルートにすべての村が含まれる」[/highlight]という制約部分閉回路(閉集合)を除去するためのペナルティー項が入っていません。とはいえ、この最後の条件を自作して反映するのは厳しいと思ったので、部分閉回路の解をあったとしても気にしないで、とりあえず1Qbitの為替アービトラージのコードの中で、入力データは美しい村間の移動距離、そして最適化のための目的関数およびペナルティ項は以下のように設定してプログラムを動かすことにしました。
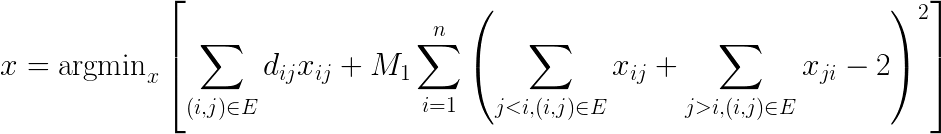
この部分に該当する箇所をコードのみ改良し、それ以外のところはそのまま利用することにしました。
しかし、まず試しに適当なデータを利用して、5個の村バージョンで計算しようとしましたが、いろいろ試しても「もっともらしい解はない!(No feasible solutions found!)」の表示しか出ないで結局挫折。このSDKにあるminimizeという関数では、どうやら村間の移動の「向き」も区別されるようで、したがって仮に解が見つかったとしても、時計回りおよび反時計周りルートの2つ最適解が存在するため、なのでしょうか、こんな簡単が問題でも解けないみたいなのです。
もちろん僕自身の理解力がないだけのせいかもしれませんが、いずれにしても、この1QbitのSDKは立ち上がったばかり。そしてこのSDKを用いた量子アニーリングによる巡回セールスマン問題のサンプルはまだ公開されていないなど、とにかく情報が少ないです。ただ、巡回セールスマン問題は、量子アニーリングの応用例としてはもっとも代表的な例と言えるので、近い将来この1Qbit SDKによるサンプルコードが誰かの手によって公開されることに期待しましょう。もちろん、もっと別の新しい応用について研究が盛んになることも期待しています。
最後にそんな期待を込めてこんな記事も紹介しておきましょう。集え、物理出身者たち!
wired.jpより:人工知能がもたらす「新しいエンジニア」の時代には、物理学者がテック業界を支配する
まとめ、感想など
ということで、2017年も引き続き話題になるであろう「量子アニーリング方式による量子コンピューター」について勉強し、実際にその効果を体験しました。従来コンピューターでの再現、量子モンテカルロ法による再現では時間がかかりすぎることは実感しました。
量子コンピュータはハード面だけでなくソフトウェア面でもその応用技術に関しての研究が思った以上に進んでいることを、具体的に知ることができました。ソフト面に関しては、今後も今回ご紹介の1Qbit社を中心に様々なアイデアが出てくることが期待されます。合わせて1Qbit SOFTWARE DEVELOPMENT KITもより拡張されることを願っています。
そして、今回、この量子アニーリングを理解するために、久しぶりに統計力学を勉強し直しましたが、大学の頃しっかりと学んでいたこともあり、思い出すのにそう時間はかかりませんでした。よって、この量子アニーリングも比較的苦労せず理解できました。
統計力学は、統計学の理解だけでなく、最近流行りの機械学習の理論にも関連することが多いので、予想外に金融の仕事上でも役立っています。今更ながら、よい学問を専攻したと満足しています。